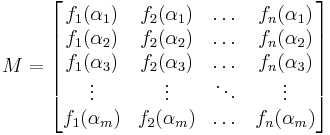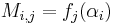Alternant matrix

In linear algebra, an alternant matrix, is a matrix with a particular structure, in which successive columns have a particular function applied to their entries. An alternant determinant is the determinant of an alternant matrix. Such a matrix of size m × n matrix may be written out as

M=\begin{bmatrix} f_1(\alpha_1) & f_2(\alpha_1) & \dots & f_n(\alpha_1)\\ f_1(\alpha_2) & f_2(\alpha_2) & \dots & f_n(\alpha_2)\\ f_1(\alpha_3) & f_2(\alpha_3) & \dots & f_n(\alpha_3)\\ \vdots & \vdots & \ddots &\vdots \\ f_1(\alpha_m) & f_2(\alpha_m) & \dots & f_n(\alpha_m)\\ \end{bmatrix}

or more succinctly

M_{i,j} = f_j(\alpha_i)

for all indices i and j. (Some authors use the transpose of the above matrix.)

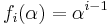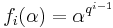Examples of alternant matrices include Vandermonde matrices, for which f_i(\alpha)=\alpha^{i-1} and Moore matrices for which f_i(\alpha)=\alpha^{q^{i-1}}.

If 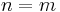n = m and the 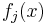f_j(x) functions are all polynomials we have some additional results: if 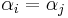\alpha_i = \alpha_j for any 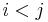i < j then the determinant of any alternant matrix is zero (as a row is then repeated), thus 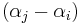(\alpha_j - \alpha_i) divides the determinant for all 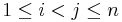1 \leq i < j \leq n. As such, if we take

V = \begin{bmatrix} 1 & \alpha_1 & \dots & \alpha_1^{n-1} \\ 1 & \alpha_2 & \dots & \alpha_2^{n-1} \\ 1 & \alpha_3 & \dots & \alpha_3^{n-1} \\ \vdots & \vdots & \ddots &\vdots \\ 1 & \alpha_n & \dots & \alpha_n^{n-1} \\ \end{bmatrix}

(a Vandermonde matrix) then 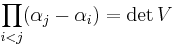\prod_{i < j} (\alpha_j - \alpha_i) = \det V divides such polynomial alternant determinants. The ratio 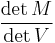\frac{\det M}{\det V} is called a bialternant. In the case where each function 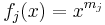f_j(x) = x^{m_j}, this forms the classical definition of the Schur polynomials.

Alternant matrices are used in coding theory in the construction of alternant codes.

See also

References